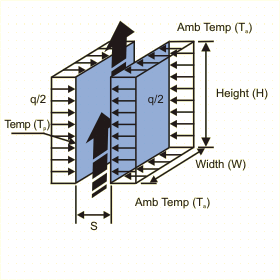
This page calculates the average heat transfer coefficient and surface temperature for an isoflux (constant and uniform flux) parallel plate vertical channel open to ambient from both ends in a natural convection environment. The convection calculation are based on Rayleigh number.
The calculation is based on Nusselt number correlations.
The temperature of the plates (Tp) is calculated as:
Tp = Ta + q / h A
Where h is the average heat transfer coefficient, A is the area of the two parallel plates, Tp is the temperature of the plates and Ta is the ambient fluid temperature. h is defined as:
h = Nu k / S
Where Nu is the Nusselt Number, k the conductivity of the fluid and H the height of the channel. The Nusselt number is calculated as:
Nu = { 48 / (Ras* S/L) + 2.51 (Ras*
S/L)(2/5) }-0.5
where Ras* = gBq"rho2CpS4 /
k2µ
Ras* (S/L) <= 10 corresponds to the fully developed
case and
Ras* (S/L) >= 100 correspond to the isolated plate
limit, i.e. for short channel or large spacing independent boundary layers
develop on each plate, and the conditions are those of an isolated plate in a
quiescent medium.
For the above equations Ras* is the Rayleigh number, g the gravitational acceleration, B the coefficient of thermal expansion, k the thermal conductivity, a the thermal diffusivity and v the kinematic viscosity.
In addition, you must define the fluid properties at the film temperature Tf defined as follows:
Tf = (Tp + Ta) / 2
References
Bar-Cohen, A., and W.M. Rohsenow, AThermally Optimum Spacing of Vertical Natural Convection Cooled, Parallel Plates, J. Heat Transfer, 106, 116 1984.
Incropera, De Witt., Fundamentals of Heat and Mass Transfer, 3rd ed., John Wiley & Sons, p557, eq.9.46, 1990.