Close

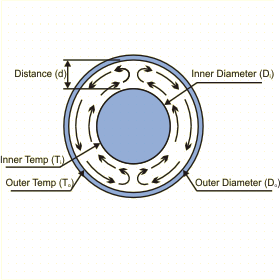
This page calculates the natural convection heat transfer between two concentric cylinders maintained at constant temperatures. The calculation is based on Rayleigh number and is valid for Rayleigh numbers below 10⁷. 

The heat transfer between the cylinders (q_c) is calculated as:

q_c = 2Pi L k_eff (T_i - T_o) / ln(D_o/D_i)

Where L is the length of the cylinders, T_i is the temperature of the inner cylinder and T_o is the temperature of the outer cylinder, where k_eff is calculated as:

k_eff  / k = 0.386(Ra_c^*)^1/4(Pr / (0.861+Pr))^1/4 
where Ra_c^* = Ra_d (ln(D_o/D_i))⁴ / (d³(D_i^-3/5+D_o^-3/5)⁵)
Ra_d = gB rho²C_p(T_i-T_o)d³ / k�

For the above equations Ra_d is the Rayleigh number based on the distance R_o-R_i, i.e. the difference between the radius of the outer cylinder and the inner cylinder, g the gravitational acceleration, B the coefficient of thermal expansion, k the thermal conductivity, Pr the Prandtl number, a the thermal diffusivity and � the dynamic viscosity. The equation for k_eff is valid between 10² < Ra_c^* < 10⁷. For values below 10², k_eff = k.   

In addition, you must define the fluid properties at the film temperature T_f defined as follows, except for the density which is defined at the reference temperature of 20 C.

T_f = (T_p + T_a) / 2

The fluid density at the film temperature is automatically calculated from the following relationship based on the perfect gas law:

 Rho = Rho_ref (T_ref +273) / (T_f + 273)

References

Raithby, G. D., and K. G. T. Hollands, A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems, in T. F. Irvine and J. P. Hartnett, Eds., Advances in Heat Transfer, Vol. 11, Academic Press, New York, pp 265-315, 1975.

Incropera, De Witt., Fundamentals of Heat and Mass Transfer, 3rd ed., John Wiley & Sons, p563, eq 9.58-9.60, 1990.