Close

This page calculates the mean heat transfer coefficient for simultaneously developing velocity and temperature fields in a circular smooth tube assuming a square abrupt entry. The convection calculation automatically switches between laminar and turbulent convection correlations based on Reynolds number. The correlations used apply for both uniform heat flux and temperature in the turbulent regime. In the laminar regime a correlation based on constant temperature is assumed.   

The calculation is based on a mean Nusselt.

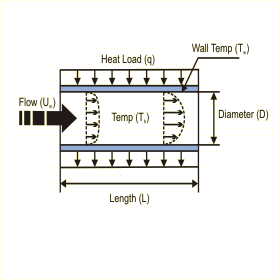
The tube wall temperature (T_w) is calculated as:

T_w = T_b + q / (h_m*A)

Where h_m is the average heat transfer coefficient between the entry and distance L, A is the surface area of the tube, q is the heat load uniformly distributed on the tube surface and T_b is the fluid bulk temperature. h_m is defined as:

h_m = Nu_m k / D

Where Nu_m is the mean Nusselt Number, k the conductivity of the fluid and D the diameter of the tube. The Nusselt number is calculated as:

For Laminar Flow - Re < 2300
If (Re Pr / L / D)^(1/3) ( �/ �_w )^0.14 >= 2.0 ; flow is developing.
    Nu_m = 1.86 (Re Pr / (L/D) )^(1/3) (� / �_w)^0.14  
        valid for 0.48 < Pr < 16,700 and 0.0044 < (� / �_w)^0.14 < 9.75 
Else ; flow is fully developed
    Nu_m = 3.66 ; uniform temperature

For Turbulent Developing Flow - 2300 < Re < 5 x 10⁶ 
    Nu_m = Nu_dev ( 1 + 2.4254 / ( L / D )^0.676) ; valid for Pr = 0.7, i.e. air
        where    Nu_dev = ( f / 8) ( Re - 1000 ) Pr / { 1 + 12.7( f / 8 )^1/2 (  Pr^2/3 - 1 ) }
        valid for 0.5 < Pr < 2,000
        and  f = ( 0.79ln Re - 1.64 ) ^-2 are the Nusselt and friction values for fully developed flow

Where Re is the Reynolds number and Pr is the Prandtl number are calculated using fluid properties as follows:

Re = fluid density x fluid velocity x diameter / dynamic viscosity
Pr = Specific heat x dynamic viscosity / thermal conductivity
� = dynamic viscosity of the fluid
�_w = dynamic viscosity evaluated at the temperature of the wall

In addition, you must define all fluid properties at the film temperature T_f defined as shown below except for �_w which is evaluated at T_w:

T_f = (T_w + T_b) / 2

References

Gnielinski, V., Int. Chem. Eng., 16, 359, 1976

Incropera, De Witt., Fundamentals of Heat and Mass Transfer, 3rd ed., John Wiley & Sons, eq.8.57, 8.63a & 8.63b, 1990.

Rohsenow, W. R., J. P. Hartnett and Y. I. Cho, Handbook of Heat Transfer, 3rd ed., McGraw Hill, 1998, p. 5.29.