Close

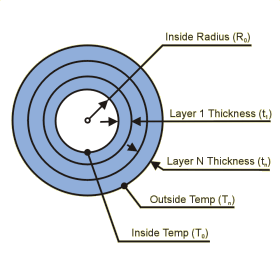
This page calculates the exterior wall temperature (T_n) for an isothermal (constant temperature) multilayer cylinder. You must define the heat load (Q) conducted from the interior to the exterior layers as well as the temperature of the interior wall (T₀) . The temperature on the exterior cylinder face is calculated. For each layer you must define the layer thickness (t_i) as well as the layer conductivity k_i.

The temperature (T_n) is calculated as:

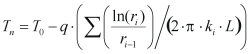
Where T₀ is the inner surface temperature, Q is the heat flow (positive heat flow is from T₀ to T_n), r_i is the outer radius of the layer i, r_i-1 is the inner radius of the layer i, k_i is the thermal conductivity of layer i, and L is the length of the cylinder. The end walls of the cylinder are assumed adiabatic. That is, only radial heat flow is accounted for.

Positive values of heat (Q) result in T₀ being hotter than T_n. Negative values of heat (Q) result in T₀ being cooler than T_n.

References

Holman, J.P., Heat Transfer, 7th ed., McGraw Hill Book Company, New York, 1990, p 30-32.